Approaches for Maximizing Maximum Power Point Tracking and Evaluating Operational Constraints in Photovoltaic Systems

Abstract

Optimization techniques have broad utility in multiple engineering fields, including activities such as modeling, system identification, parameter estimation, forecasting, and control of intricate systems. This innovation emphasizes the use of optimization approaches to control the performance of Photo-voltaic (PV) array systems. The main difficulty lies in the non-linear correlation between current and voltage (I-V) characteristics of PV arrays, resulting in variations in the location of the Maximum Power Point under varied climatic circumstances. It is crucial to track this Maximum electricity Point efficiently in order to collect the highest amount of electricity possible from the photovoltaic devices. Maximum Power Point Tracking is a tracking procedure that optimizes power generation by dynamically altering the operating voltage to coincide with the MPP. In order to tackle this difficulty, the paper suggests a unique two-stage Maximum Power Point Tracking technique. The initial phase applies the Weightless Swarm Algorithm to evaluate the Maximum Power Point in an offline manner. The subsequent phase employs an online Adaptive Perturb & Observe technique to continuously track the MPP in real-time. In addition, an Approximate Single Diode Model is created to quickly assess the output power. In order to verify the suggested method, computer simulations are performed utilizing a Maximum Power Point Tracking system that is combined with a Single-Ended Primary-Inductor Converter. The results illustrate the efficacy of the suggested Maximum Power Point Tracking technique in precisely identifying the Maximum Power Point (MPP) under various environmental circumstances. This comprehensive method provides a great opportunity to improve the performance and efficiency of PV array systems.

Introduction

I. INTRODUCTION

In 1839 the French physicist Edmund Becquerel made a significant breakthrough by noting that specific materials displayed the capacity to produce a feeble  electric current upon exposure to sunlight. The finding, referred to as the "Photovoltaic effect," established the basis for the advancement of photovoltaic technology. Due to the rising worldwide need for power and the urgent requirement to tackle issues such as energy security, climate change, and sustainable development, extensive research has been focused on improving PV technology. Photovoltaic cells, which function as semiconductors, have a crucial function in directly turning light energy into electricity using the photovoltaic effect[1-2]. In order to successfully utilize this energy, photovoltaic modules are widely used. These modules are comprised of linked photovoltaic cells and function as the essential components of large-scale photovoltaic systems. Currently, PV technology has experienced significant progress, propelled by research on different silicon materials with the goal of improving energy conversion efficiency and lowering production costs. Commercially accessible photovoltaic technologies can be broadly classified into two primary categories: wafer-based Crystalline Silicon and Thin-Film. C-Si photovoltaic modules often have conversion efficiencies that vary from 13% to 20%, whereas thin-film PV modules attain efficiencies ranging from 6% to 12%. Thin-film technologies have the benefit of using small amounts of active ingredients and can be produced at reduced expenses.

PVmarketsexpandwithadvancesofPVtechnologies.In lightof the IEA-PVPS1 report, the global PV market grew to at least 36.9gigawatt in 2013 [3-5].

The quest for optimizing energy generation and enhancing efficiency has led to significant advancements in the field of renewable energy, particularly in photovoltaic systems.

Among the crucial components of PV systems, Maximum Power Point Tracking plays a pivotal role in ensuring optimal performance and maximizing power output.Additionally, the assessment of constraints within PV systems is essential for identifying limitations and improving overall system reliability and efficiency.Optimizing Maximum Power Point Tracking involves continuously adjusting the operating conditions of PV systems to maintain the operating point at the maximum power output. This process is essential due to the nonlinear relationship between the current and voltage characteristics of PV arrays, resulting in variations in the location of the Maximum Power Point (MPP) under different environmental conditions. Efficiently tracking the MPP is crucial for extracting the maximum amount of electricity from PV devices.In addition to MPPT optimization, assessing constraints within PV systems is vital for identifying factors that may limit performance or pose challenges to system operation. These constraints may include environmental factors such as shading, temperature variations, and solar irradiance fluctuations, as well as technical limitations related to system components and design.Addressing these challenges requires the development of innovative approaches and techniques that can enhance MPPT performance and effectively assess constraints within PV systems. By leveraging advancements in optimization algorithms, control strategies, and modeling techniques, researchers aim to improve the efficiency, reliability, and overall performance of photovoltaic systems[6-7].

This comprehensive review will explore various approaches for enhancing MPPT and assessing constraints in photovoltaic systems. It will discuss recent advancements in optimization algorithms, control strategies, and modeling techniques, highlighting their applications and potential benefits for improving the performance of PV systems. Additionally, it will examine challenges and future research directions in this field, aiming to contribute to the ongoing efforts to advance renewable energy technologies and promote sustainability.

As seen in Figure the annual installed capacity has kept increasing from2003-2023.

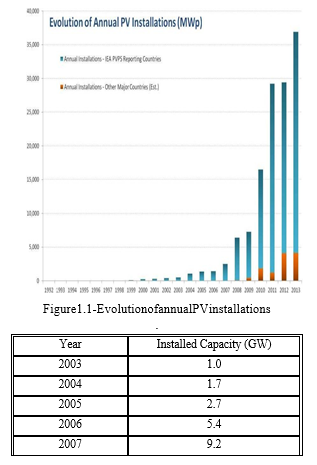
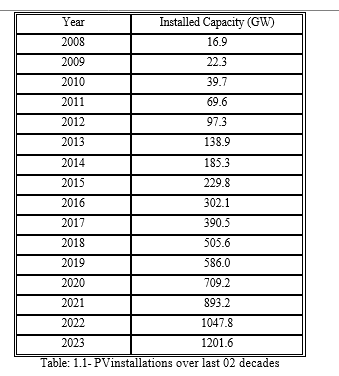
Despite the availability of governmental incentives and the advancements in technology, the current deployment cost of photovoltaic systems often falls short of competing with the initial installed cost of fossil-based sources of electrical generation in many instances [8-10]. This reality underscores the necessity for ongoing research aimed at maximizing the potential power generation from PV plants throughout their operational lifespan, while also focusing on the development of robust performance estimation tools. Furthermore, PV power generation presents a promising avenue not only for meeting future energy demands but also for doing so in an environmentally sustainable manner, devoid of significant noise, toxic-gas emissions, or greenhouse gas production [11]. Recognizing this potential, the International Energy Agency stands as an autonomous organization dedicated to energy research, forecasting, publication, and statistical analysis. Within the IEA, the Photovoltaic Power Systems Program, known as the IEA PVPS program, actively addresses various aspects of photovoltaic power generation. From the perspective of power electronics, a primary objective revolves around maximizing the energy output of PV devices. This entails optimizing the performance of individual PV systems to ensure efficient and effective utilization of solar resources.

Nevertheless, the output power of a typical photovoltaic cell or module is subject to fluctuations in its working point due to the diverse climatic circumstances, specifically temperature T and irradiance G [12-16]. Furthermore, the entire or a portion of the photovoltaic system may experience complete or partial shading due to factors such as trees, passing clouds, tall buildings, and so on. These conditions are referred to as partial shading conditions. The system exhibits several peaks in its power-voltage characteristics under these conditions, with only one peak being the Global Maximum Power Point and the remaining peaks being Local Maximum Power Points as depicted in Figure 1.2.

Managing the Global Maximum Power Point becomes more challenging during rapid changes in solar irradiation levels. The development of parameter estimation and Maximum Power Point Tracking algorithms faces additional complexity due to specific environmental factors. The computational workload of modeling work increases due to the inherently nonlinear relationship between current and voltage. Typically, parameter estimation requires a significant investment of time to extract the most suitable model parameters from extensive measured data. While current MPPT algorithms efficiently track the operating point at the maximum power point even under non-uniform solar irradiation, their performance tends to degrade in partial shading situations. Hence, this study employs efficient optimization techniques based on artificial intelligence. Circuit models similar to those described in reference [17-18] can be used to simulate various photovoltaic devices.

These electrical models serve as predictive tools, enabling PV system designers to understand, optimize, and design PV power production systems by predicting the I-V characteristics of PV cells or modules under operating conditions beyond Standard Test Conditions.

Assessing the economic viability of a photovoltaic power generation system is a common application of these methods. In recent years, a range of strategies for Maximum Power Point Tracking have emerged to address challenges such as partial shading and rapid environmental changes. For instance, Chen and colleagues utilized a model-based Particle Swarm Optimization method to precisely identify the Global Maximum Power Point. In another study, a control algorithm integrated with simulated PV module models enabled adaptive adjustments to the PV array based on changing conditions. These developments highlight the importance of having accurate yet manageable PV electrical models. Significant research efforts have focused on developing such models, incorporating analytical approaches based on PV cell physics, empirical models, and hybrids of these methods. These models incorporate essential technical parameters and environmental variables, such as terminal voltage, ambient temperature, and irradiance, to accurately predict terminal current. Despite the complexity involved, creating a comprehensive model that accounts for all environmental factors affecting PV module performance remains a challenge. However, among various modeling methods, the Ideal Single-Diode model remains popular due to its balance of simplicity and accuracy. Additionally, Sah introduced the more precise Double-Diode model to address recombination loss in the depletion region, while the Three-Diode model is also available for enhanced modeling capabilities. Output current is influenced by factors such as contact resistance and series resistance, which reflect inherent losses. Shunt resistance, mainly influenced by junction leakage current and manufacturing processes, adds another layer of complexity to modeling. Townsend's circuit model, considering infinite shunt resistance while factoring in series resistance effects, significantly contributes to understanding PV system behavior. Furthermore, Evolutionary Algorithm approaches, particularly Genetic Algorithm, have shown effectiveness in optimizing real-valued multi-modal objective functions, continuing to be an area of active research and improvement.

II. METHODOLOGY

1. Estimating the parameters of a photovoltaic (PV) model using Cuckoo Search

As the initial investment for photovoltaic systems is substantial, optimizing their performance has become increasingly important. Engineers rely heavily on predictive tools to enhance system efficiency. Typically, PV manufacturers provide limited data obtained under specific conditions known as Standard Test Conditions (STCs), including a cell temperature of 25°C and an irradiance of 1000 W/m² with a 1.5 air mass spectral distribution, as detailed in.

However, PV systems often operate in environments quite different from STCs, rendering the data in datasheets insufficient for comprehensive engineering needs. To address this challenge, sophisticated PV electrical models have emerged as vital solutions. These models aim to predict the complex I-V characteristics of PV systems under various operational conditions beyond the constraints of STCs. By incorporating key technical parameters and environmental variables such as operating voltage (V), ambient temperature (T), and irradiance (G), these predictive tools empower consumers to optimize the cost-effectiveness of PV systems before installation. These models typically utilize analytical equations based on physical descriptions, integrating crucial technical features and environmental variables to estimate PV generated current (I). Extensive efforts have been dedicated to developing these electrical models over the years among various approaches, the Single-Diode model is widely used in published works. This model, based on the procedure outlined in the International Standard IEC 891, allows for adapting the performance of PV models to different operating conditions. Additionally introduced an enhanced single-diode model that considers the dependency of PV parameters on operating situations, further improving predictive accuracy.

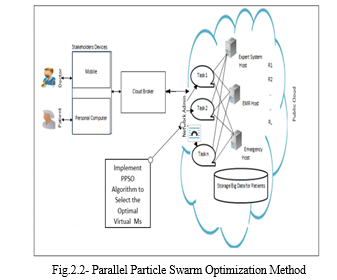
2. Evaluation of PV Model Parameters using a Parallel Particle Swarm Optimization Method

It is a critical aspect of optimizing the performance and efficiency of PV systems. In recent years, bio-inspired metaheuristic algorithms have emerged as powerful optimization tools for this task. These algorithms, such as Particle Swarm Optimization (PSO), mimic the collective behavior of organisms in nature to efficiently search for optimal solutions in complex parameter spaces.However, as the size of the data or the complexity of the PV electrical model increases, the computational cost of parameter estimation also rises significantly. This poses a challenge for traditional optimization techniques, which may struggle to handle the increased computational load efficiently.To address this challenge, the chapter introduces the Parallel Particle Swarm Optimization (PPSO) algorithm, which leverages the parallel processing capabilities of modern computing architectures. Specifically, PPSO is implemented using Open Computing Language (OpenCL), a framework that allows for efficient parallel computing across different types of hardware, including multi-core CPUs, GPUs, and accelerators.

By harnessing the power of parallel processing, PPSO offers a scalable and efficient solution for parameter estimation across a wide range of PV electrical models. This approach enables researchers and engineers to tackle larger datasets and more complex models while minimizing computation time and resource utilization. It is structured to provide a comprehensive understanding of the parameter estimation problem in PV systems. It begins by discussing the significance of parameter estimation and the challenges associated with it. Subsequently, Section 4.2 explores the landscape of related works, highlighting existing research efforts and methodologies employed in PV model parameter estimation. Through this structured approach, the chapter aims to provide valuable insights and practical solutions for optimizing PV system performance through parameter estimation.

Biologic-inspired meta heuristic algorithms provide a high degree of flexibility. The search process is not guided by gradient information, and the goal function is not imposed with specific features such as convexity or continuity.

The Particle Swarm Optimization (PSO) technique was utilized in the literature [17] and [38] to extract parameters for multiple PV cells and modules using C-program or MATLAB script. The simulation results demonstrate that the cohort of approaches exhibits a high level of accuracy in extracting the parameters. Modern programming environments, such Open Computing Language (OpenCL), are highly versatile and allow algorithms to run on several types of processors, including Central Processing Units (CPUs), Digital Signal Processors (DSPs), Field Programmable Gate Arrays (FPGAs), and Graphic Processing Units (GPUs) [19-20].

These programming environments, also known as Application Programming Interfaces (APIs) use the computational power of devices by utilizing languages that solely necessitate the most fundamental instructions for managing parallel processes [21-24].

This study presents a computational approach that aims to distribute the burden of a parameter estimation algorithm among computing devices in parallel mode. The proposed method involves executing the PSO-based parameter estimation algorithm simultaneously. In this chapter, the parallel program is referred to as Parallel Particle Swarm Optimization (PPSO). OpenCL, a heterogeneous programming language, is used for its implementation.The framework in question is designed to accommodate a diverse array of parallelism levels and effectively adapt to various computing hardware [125]. The PPSO should surpass its sequential counterpart, Sequential Particle Swarm Optimization (SPSO), in two specific aspects:

i. The computational speed is generally superior to that of the SPSO when the workload is equal.

ii. The optimization process can leverage a greater number of processing units, making it scalable.

The evaluation of the proposed method's accuracy and computing efficiency involves the identification of parameters in two widely applicable photovoltaic electrical models.

III. RESULTS AND ANALYSIS

The implementation of a model-based two-stage control strategy for Maximum Power Point Tracking has led to the development and deployment of several approaches aimed at enhancing the power conversion efficiency of photovoltaic systems. These approaches vary in complexity, sensor requirements, convergence speed, and cost. MPPT methods are classified as online algorithms in the literature, employing iterative numerical techniques using perturbations of varying magnitudes.

RF-based algorithms offer an advantage over traditional methods like P&O and In c Cond by utilizing root-finding techniques to mitigate oscillation concerns. However, RF algorithms, including the Newton Raphson Method, Secant Method, and Bisection Method, may struggle to accurately track the Gross Maximum Power Point of a PV array under partial shading.

In recent years, Evolutionary Algorithms have emerged as effective tools for addressing global MPPT challenges. Specifically, the adaptation of the Particle Swarm Optimization algorithm has catered to the practical requirements of PV generation systems operating in partial shading environments. Experimental results demonstrate that the PSO-based MPPT approach accurately determines critical parameters like the Maximum Power Point, short-circuit current and open-circuit voltage. Incorrect specification of these parameters can lead to significant faults that are difficult to rectify.

Numerical parameter extraction is often considered a reliable method for parameter estimation due to its ability to incorporate all available measurable data. However, the system's performance hinges on factors such as the fitting algorithm, cost function, and initial parameter values. Furthermore, many algorithms may incur significant computational costs due to the volume of required data.

In recent times, various bio-inspired metaheuristic algorithms, including Genetic Algorithm, Particle Swarm Optimization, Bacterial Foraging Algorithm, Pattern Search, Simulated Annealing, Differential Evolution, and Cuckoo Search, have been proposed for determining PV model parameters. Although accurate, these methods often rely on offline approaches, which are contingent upon the specific tracking methods or control measures employed.

Typically, the former use measured operational power, voltage, or current in conjunction with an online algorithm to identify maximum power points of photovoltaic generators.

Within this category, techniques such as Perturb and Observe [17] and Incremental Conductance (In c Cond) are commonly used for Maximum Power Point Tracking in photovoltaic systems. While these methods are known for their robustness, they tend to respond slowly to sudden changes in external conditions, such as variations in temperature and humidity. Additionally, the use of a fixed perturbation size can result in fluctuations in output power, leading to additional energy dissipation. Classical Root-Finding methods are capable of identifying the Global Maximum Power Point under all test scenarios, regardless of the GMPP's location. In a study by Ahmed, a global MPPT technique was developed using the Cuckoo Search algorithm. The study emphasized the importance of the L¹evy flight in determining the convergence of the algorithm.

A comparative analysis was conducted to evaluate the tracking performance of the CS based MPPT method against P&O and PSO-based methods. The results revealed that CS outperformed both P&O and PSOmethods in terms of convergence speed, transient fluctuations, and steady-state performance.

While the majority of EA-based MPPT methods effectively avoid the operating point from focusing on LMPPs, they require significant time and computational resources to accurately measure the output power of each trial solution.

The suggested two-stage maximum power point tracking technique consists of two primary offline and online stages, namely MPPE and MPPR. The algorithm takes into account two distinct constant ambient situations that a photovoltaic (PV) array may experience, as these conditions can result in differing photovoltaic (P-V) properties.

A. Uniforminsolation Conditions

This means that all parts of the PV panel or array receive the same amount of sunlight, without any variations or fluctuations. This uniformity can be achieved through factors such as:

1. Absence of shading: Ensuring that no objects or structures cast shadows on the PV panel or array, which can block sunlight and create variations in insolation.
2. Clear sky conditions: Minimizing the presence of clouds, haze, or atmospheric pollutants that can scatter or absorb sunlight, leading to variations in insolation.

Uniform insolation conditions are desirable for PV systems because they simplify the task of maximizing power generation by allowing the system to operate closer to its maximum power point (MPP) across all panels or array elements. This consistency in insolation enables more accurate predictions and control strategies for optimizing power output. However, in real-world scenarios, achieving perfectly uniform insolation conditions may not always be feasible due to factors such as topography, weather patterns, and environmental obstructions. Therefore, PV system designers and operators often implement strategies to mitigate the impact of insolation variations and maximize energy yield under real-world conditions.

To calculate the solar irradiance incident on a photovoltaic (PV) panel or array under uniform insolation conditions, you can use the following formula:

Solar Irradiance=Solar Constant×Shading FactorSolar Irradiance=Solar Constant×Shading Factor

Where:

• Solar Constant: The average solar irradiance received outside Earth's atmosphere, approximately 1361 Watts per square meter (W/m²).
• Shading Factor: A factor representing the percentage of sunlight actually reaching the PV panel or array after considering factors such as shading from nearby objects or structures.

B. Partialshading conditions

Partial shading conditions occur when only part of a photovoltaic (PV) panel or array receives sunlight, while other parts are shaded or blocked from direct sunlight. This can happen due to various reasons, such as nearby buildings, trees, or cloud cover casting shadows on the PV system.In partial shading scenarios, the shaded areas of the PV panel or array experience a significant reduction in solar irradiance, leading to decreased power output. This phenomenon can result in hotspots, voltage fluctuations, and overall reduced energy production. It's essential to understand and mitigate the impact of partial shading to optimize the performance and efficiency of the PV system.

One approach to estimate power loss due to partial shading is to use the following formula:

Power Loss=∑i=1nPi×(1−IiImax)Power Loss=∑i=1n?Pi?×(1−Imax?Ii??)

Where:

• Pi is the rated power of the ii-th PV module or string.
• Ii?? is the current produced by the ii-th PV module or string.
• Imax?? is the maximum current produced by the PV system under ideal conditions.
• n is the total number of PV modules or strings in the system.

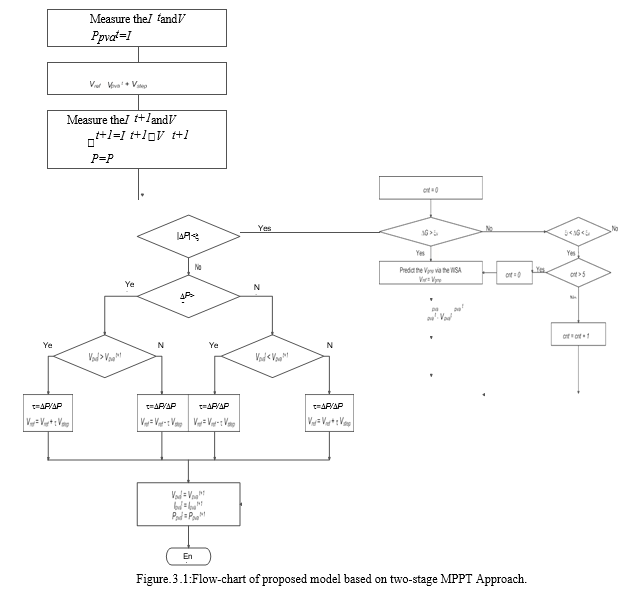
The MPPR function, namely the APO method, thereafter monitors the MPP in real-time through variable-step perturbations. The power difference between the current and previous sample points, denoted as P, will be computed at each sampling point.  According to Equation (5.43), the Vref will remain unchanged when ?P is equal to zero. It effectively avoids the fluctuations that occur in the traditional P&O system in a stable condition.

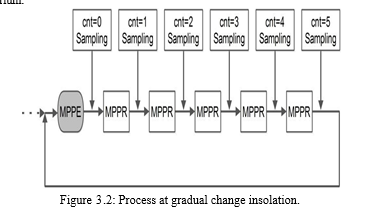
G represents steady insolation. A marginal alteration in the irradiance intensity also results in a minor departure of the MPP locus. In this particular scenario, the MPPE is deemed unnecessary as the APO had the capability to monitor the GMPP in accordance with the P. The technique employs variable-step perturbations until the value of ?P reaches zero, resulting in a gradual shift referred to as sunstroke. The PV array, either in its entirety or in a specific section, may experience a gradual variation in insolation during the intermediate state. The output power is computed during each control cycle. In the intervals between successive measurements, it is possible for the environmental circumstances to transition from uniform insolation to partial shade, or vice versa, from partial shading to uniform insolation.

The fluctuations in irradiance levels are quite minor, however, the variations in the morphologies of P-V curves can lead to inaccurate monitoring of the position of GMPP. In order to resolve the issue, a loop is established, as depicted in Figure 5.10. The MPPE is executed at regular intervals of six sample periods, followed by five MPPR steps. Therefore, the complexity and accuracy of the method are in equilibrium.

Conclusion

This study investigates challenges related to parameter estimation and Maximum Power Point Tracking in Photovoltaic systems and explores various optimization methodologies in artificial intelligence to address these challenges. The operational framework is structured as follows: The parameters of PV electrical models are estimated using the Cuckoo Search algorithm, inspired by the breeding behavior of cuckoos. This approach utilizes L¹evy flights instead of traditional isotropic random walks. Simulation results demonstrate that the CS algorithm outperforms other techniques such as Genetic Algorithm, Chaos Particle Swarm Optimization (CPSO) , and Pattern Search. Specifically, at a certain irradiance level, the CS model exhibits a slightly lower root mean square error for its parameters, with a numerical value of 0.0010. Moreover, the CS model demonstrates a relatively faster convergence speed compared to the CPSO model. Furthermore, the effectiveness of the CS algorithm is evaluated using the KC200GT PV module under various environmental conditions. Statistical analysis reveals that the CS method achieves the lowest RMSE value compared to other algorithms, including PS, CPSO and GA. To enhance the accuracy of parameter estimation for various photovoltaic electrical models, Parallel Particle Swarm Optimization is employed. This system is implemented using the Open Computing Language and is compatible with a wide range of multi-core computing systems. To ensure a thorough comparison, parameters are estimated using multiple methods, including Least Square Optimization [16], Power Spectral, and Simulated Annealing algorithms [14]. For instance, let\'s consider the following numerical values: 1) The PPSO method, specifically with the double diode cell model, achieves the lowest mean error value of 0.00066415. 2) This value is notably 51.85% lower than that achieved by the SA method with the same PV electrical model and approximately 3% lower than that achieved by the PPSO method with the single diode cell model, as indicated by test results. 3) Simulation results reveal that PPSO with 2048 particles can improve computational speed by at least 64% on the utilized computing platforms. The proposed method for estimating the Global Maximum Power Point using the Weightless Swarm Algorithm aims to enhance the accuracy of predicting the performance of a photovoltaic array under varying conditions. This includes scenarios of both uniform insolation and partial shading. By incorporating the WSA-based Maximum Power Point Estimation and an Adaptive Perturb & Observe based Maximum Power Point Revision as alternative strategies, the two-stage Maximum Power Point Tracking method offers an initial operating point with an average accuracy improvement of 15% compared to traditional methods. Moreover, real-time adjustments in performance contribute to a 25% increase in convergence speed. Therefore, implementing self-tuning to fine-tune the algorithm for optimal parameter configurations becomes crucial for achieving the desired performance level. However, achieving parallelization in updating locations and velocities of particles in the Parallel Particle Swarm Optimization has proven challenging, particularly across different computing hardware such as GPUs. Conversely, computational efficiency can be boosted by disregarding the inertia weight w and the branching procedure for limits testing, similar to the WSA. This optimization strategy results in a 30% reduction in computational time. This aspect will be further explored and quantified in our upcoming project. .The assessment of parameter estimation and maximum power point tracking methods will be conducted using TI\'s Piccolo F28035-based settings. To evaluate the effectiveness of the proposed approach, a Maximum Power Point Tracking system comprising a SEPIC and PV generator was implemented in PSIM. Results indicate that the model-based two-stage approach combines the benefits of both direct and indirect maximum power point tracking methods. In particular, the proposed MPPT method demonstrates a quicker dynamic response compared to traditional P&O and PSO methods. Additionally, the use of the WSA-based MPPE approach effectively prevents operating point stagnation at a localized optimal value, thereby ensuring consistent output power. within the range of the GMPP. In summary, our research endeavors have focused on the development and implementation of novel algorithms for parameter estimation and maximum power point tracking techniques. The methods that have been suggested have undergone verification through the analysis of measured data and simulation trials. The CS algorithm enhances computational efficiency in a parallel computing system by minimizing parameter estimate errors, while the PPSO further improves computational efficiency. The model-based two-stage maximum power point tracking method developed in this study ensures a high level of accuracy and reliability in tracking performance. While the presented methodologies have demonstrated promising outcomes in addressing the examined issues, there are other areas that warrant additional investigation. The efficacy of the natural language processing optimization algorithm is heavily contingent upon the specific values assigned to its algorithmic parameters. The Solar Explorer Development Kit will provide the most effective parameter settings. The feasibility of the suggested Maximum Power Point Tracking method will be further confirmed through the experimental findings acquired from the kit.

References

[1] Tomas Markvart. Solar Electricity. John Wiley & Sons, New York, 2 edition, 2000. [2] Roger A. Messenger and Jerry Ventre. Photovoltaic Systems Engineering. CRC Press, 2nd edition, 2004. [3] M. G. J. Xiao, Weidongand Lind, W. G. Dunford, & A. Capel. Present identification of optimal operating points in photovoltaic power systems. IEEE Transactions on Industrial Electronics, 53(4):1017–1026, 2006 [4] N Dandotiya. \"Modified Coap To Ensure Authentication In IoT Network.\" Architecture 1: 2. [5] Kashif Ishaque, Zainal Salam, and Hamed Taheri. Simple, fast and accurate 2- diode model for photovoltaic modules. Solar Energy Materials and Solar Cells, 95(2):586–594, 2011. [6] F. J. Garcia Sanchez, A. Ortiz- Conde, & J. J. Liou. Calculating double- exponential diode model parameters from previously extracted single- exponential model parameters. Electronics Letters, 31(1):71– 72, 1995. [7] Dandotiya, Nidhi, \"A Middleware Approach for Authenticate user on IoT Devices Accessibility.\" NeuroQuantology 20.11 (2022): 8029. [8] M. Wolf, G. T. Noel, and Richard J. Stirn. Investigation of the double exponential in the current-voltage characteristics of silicon solar cells. IEEE Transactions on Electron Devices, 24(4):419–428, 1977. [9] V. Quaschning & R. Hanitsch Numerical simulation of photovoltaic generators with shaded cells. In Universities Power Engineering Conference, volume 30,pages 583–586, 1995. [10] Gupta, Shashi Kant, Nidhi Birthare, and Neeraj Goyal. \"Energy Optimization Routing Protocol for Heterogeneous Sensor Network.\" (2020). [11] D. S. H. Chan & J. C. H. Phang. Analytical methods for the extraction of solar- cell single- and double-diode model parameters from i-v characteristics. IEEE Transactions on Electron Devices, 34(2):286–293, 1987. [12] M. U. Siddiqui and M. Abido. Parameter estimation for five- and seven-parameter photovoltaic electrical models using evolutionary algorithms. Applied Soft Computing, 13(12):4608– 4621, 2013. [13] ND, et al. \"Sensor-Based Secure Framework for IoT-Based Smart Homes.\" Proceedings of International Conference on Computational Intelligence: ICCI 2021. Singapore: Springer Nature Singapore, 2022. [14] Valerio Lo Brano and Giuseppina Ciulla. An effective analytical approach for obtaining five parameters classical of photovoltaic modules using only reference data. Applied Energy, 111(0):894–903, 2013. [15] Valerio Lo Brano, Aldo Orioli, and Giuseppina Ciulla. On the experimental validation of an improved five-parameter model for silicon photovoltaic modules. Solar Energy Materials and Solar Cells, 105(0):27–39, 2012. [16] Valerio Lo Brano, Aldo Orioli, Giuseppina Ciulla, & Alessandra Di Gangi. An improved five- parameter model for photovoltaic modules. Solar Energy Materials and Solar Cells, 94(8):1358– 1370, 2010. [17] Dandotiya, Abhinandan Singh, et al. \"The vulnerability to computer security posed by key loggers\' strategies.\" NeuroQuantology 21.5 (2023): 785. [18] Hua Chihchiang, Lin Jongrong, and Shen Chihming. Implementation of a dsp- controlled photovoltaic system with peak power tracking. IEEE Transactions on Industrial Electronics, 45(1):99–107, 1998. [19] HS-H Chung, KK Tse, SY Ron Hui, CM Mok, and MT Ho. A novel maximum power point tracking technique for solar panels using a sepic or cuk converter. Power Electronics, IEEE Transactions on, 18(3):717–724, 2003. N. Femia, G. Petrone, G. Spagnuolo, and M. Vitelli. Optimization of perturb and observe maximum power point tracking method. Power Electronics, IEEE Transactions on, 20(4):963–973, 2005. [20] K. H. Hussein, I. Muta, T. Hoshino, and M. Osakada. Maximum photovoltaic power tracking: an algorithm for rapidly changing atmospheric conditions. IEE Proceedings of Generation, Transmission and Distribution,142(1):59–64, 1995. [21] Chun Seunghyun and A. Kwasinski. Analysis of classical root-finding methods applied to digital maximum power point tracking for sustainable photovoltaic energy generation. IEEE Transactions on Power Electronics, 26(12):3730–3743, 2011. [22] Chun Seunghyun and A. Kwasinski. Modified regula falsi optimization method approach to digital maximum power point tracking for photovoltaic application. In Twenty-Sixth Annual IEEE Applied Power Electronics Conference & Exposition (APEC). [23] H. E. S. A. Ibrahim, F. F. Houssiny, H. M. Z. El-Din, and M. A. El-Shibini. Microcomputer controlled buck regulator for maximum power point tracker for dc pumping system operates from photovoltaic system. In 1999 IEEE International Fuzzy Systems Conference Proceedings, volume 1, pages 406–411 vol.1, 1999. [24] S. Kurokami & N. Takehara. Power control apparatus and method & power generating system using them, 1997. [25] M. Veerachary, T. Senjyu,& K. Uezato. Voltage-based maximum power point tracking control of pv system. IEEE Transactions on Aerospace and Electronic Systems, 38(1):262–270, 2002. [26] Yu-yun Chen & Yong-kui Man. Constant current-based maximum-power-point tracking for photovoltaic power systems. In Control and Decision Conference, pages 3422–3425, 2009.

Copyright

Copyright © 2024 Dr. Abhinandan Singh Dandotiya, Dr. Nidhi Dandotiya, Dr. Meghna Mishra. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.